1. Home
2. C Programming Examples
3. C Program to determine the type and Area of a Triangle

C Program to determine the type and Area of a Triangle

Last updated on July 27, 2020

The following is a C Program to determine the type and Area of a Triangle:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

/*****************************************************
 Program to determine the type and area of a triangle
 *****************************************************/

#include<stdio.h> // include stdio.h library
#include<math.h> // include math.h library

int main(void)
{   
    float a, b, c, s, area;

    printf("Enter sides of a triangle: \n");

    printf("a: ");
    scanf("%f", &a);

    printf("b: ");
    scanf("%f", &b);

    printf("c: ");
    scanf("%f", &c);

    // sum of any two sides must be greater than the third side    
    if( (a + b > c) && (b + c > a) && (c + a > b) )
    {
        //  three sides are equal
        if( (a == b) && (b == c) )
        {
            printf("Triangle is equilateral.\n");
        }

        //  two sides are equal
        else if( (a == b) || (b == c) || (a == c) )
        {
            printf("Triangle is isosceles.\n");
        }

        // no sides are equal
        else
        {
            printf("Triangle is scalene.\n");
        }

        //  area of triangle using heron's formula https://en.wikipedia.org/wiki/Heron's_formula

        s = (a + b + c) / 2;  //semi perimeter

        area = sqrt(  s * (s - a) * (s - b) * (s - c) ); // area

        printf("Area of triangle %.2f.", area);

    }

    else
    {
        printf("Sides don't make a triangle.");
    }

    return 0; // return 0 to operating system
}

Expected Output:

1st run:

1
2
3
4
5
6

Enter sides of a triangle: 
a: 3
b: 4
c: 5
Triangle is scalene.
Area of triangle 6.00.

2nd run:

1
2
3
4
5

Enter sides of a triangle: 
a: 4
b: 5
c: 1
Sides don't make a triangle.

How it works #

The above program uses two theorems:

• Triangle Inequality Theorem
• Heron's Formula

Triangle Inequality Theorem #

The Triangle Inequality Theorem states that the sum of two sides of a triangle must be greater than the third side.

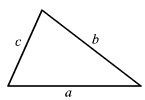
Let a, b c be the three sides of the triangle then according to Triangle Inequality theorem:

1
2
3

a + b > c
b + c > a
c + a > b

We can also use Triangle Inequality theorem to determine whether the given three line segments can be used to construct a triangle or not.

In order for three line segments to form the sides of a triangle, all the three conditions must be satisfied.

If any one of the condition fails then the given line segments can't be used to construct a triangle. For example:

Example 1: Can we construct a triangle using the following lengths: 7, 3, 2?

1
2
3

7 + 3 > 2 => true 
3 + 2 > 7 => false
7 + 2 > 3 => true

The second condition is false. Hence, lengths 7,3 and 2 can't construct a triangle.

Example 2: Can we construct a triangle using the following lengths: 3, 4, 5?

1
2
3

3 + 4 > 5 => true  
4 + 5 > 3 => true
5 + 3 > 4 => true

All the three conditions are true. Hence, lengths 3, 4, 5 can be used to construct a triangle.

Heron's Formula #

Heron's Formula allows us to find the area of the triangle using the length of the three sides.

\begin{gather*}
Area=\sqrt{s(s-a)(s-b)(s-c)}
\end{gather*}

where s is called the semi perimeter of the triangle and is calculated as follows:

\begin{gather*}
s=\frac{a+b+c}{2}
\end{gather*}