1. Home
2. C Programming Tutorial
3. Pointers and 2-D arrays

Pointers and 2-D arrays

Last updated on July 27, 2020

In the last chapter, we have created a pointer which points to the 0th element of the array whose base type was (int *) or pointer to int. We can also create a pointer that can point to the whole array instead of only one element of the array. This is known as a pointer to an array. Here is how you can declare a pointer to an array.

int (*p)[10];

Here p is a pointer that can point to an array of 10 integers. In this case, the type or base type of p is a pointer to an array of 10 integers.

Note that parentheses around p are necessary, so you can't do this:

int *p[10];

here p is an array of 10 integer pointers. An array of pointers will be discussed in upcoming chapters.

A pointer that points to the 0th element of an array and a pointer that points to the whole array are totally different. The following program demonstrates this concept.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include<stdio.h>

int main()
{
    int *p; // pointer to int
    int (*parr)[5]; // pointer to an array of 5 integers
    int my_arr[5]; // an array of 5 integers

    p = my_arr; 
    parr = my_arr;

    printf("Address of p = %u\n", p );
    printf("Address of parr = %u\n", parr );

    p++;
    parr++;

    printf("\nAfter incrementing p and parr by 1 \n\n");
    printf("Address of p = %u\n", p );
    printf("Address of parr = %u\n", parr );

    printf("Address of parr = %u\n", *parr );

    // signal to operating system program ran fine
    return 0;
}

Expected Output:

1
2
3
4
5
6
7

Address of p = 2293296
Address of parr = 2293296

After incrementing p and parr by 1

Address of p = 2293300
Address of parr = 2293316

How it works:

Here p is a pointer which points to the 0th element of the array my_arr, while parr is a pointer which points to the whole array my_arr. The base type of p is of type (int *) or pointer to int and base type of parr is pointer to an array of 5 integers. Since the pointer arithmetic is performed relative to the base type of the pointer, that's why parr is incremented by 20 bytes i.e ( 5 x 4 = 20 bytes ). On the other hand, p is incremented by 4 bytes only.

The important point you need to remember about pointer to an array is this:

Whenever a pointer to an array is dereferenced we get the address (or base address) of the array to which it points.

So, on dereferencing parr, you will get *parr. The important thing to notice is although parr and *parr points to the same address, but parr's base type is a pointer to an array of 5 integers, while *parr base type is a pointer to int. This is an important concept and will be used to access the elements of a 2-D array.

Pointers and 2-D Array #

While discussing 2-D array in the earlier chapters, we told you to visualize a 2-D array as a matrix. For example:

1
2
3
4
5

int arr[3][4] = {
                    {11,22,33,44},
                    {55,66,77,88},
                    {11,66,77,44}
                };

The above 2-D array can be visualized as following:

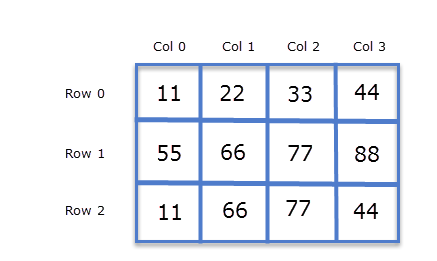
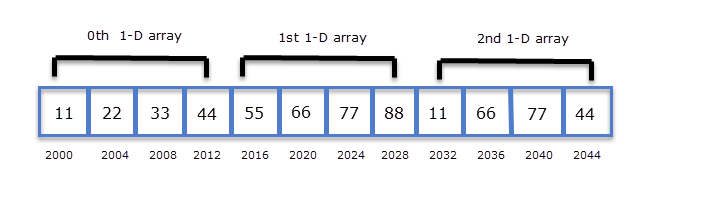
While discussing array we are using terms like rows and column. Well, this concept is only theoretical, because computer memory is linear and there are no rows and cols. So how actually 2-D arrays are stored in memory ? In C, arrays are stored row-major order. This simply means that first row 0 is stored, then next to it row 1 is stored, next to it row 2 is stored and so on.

The following figure shows how a 2-D array is stored in the memory.

Here is the most important concept you need to remember about a multi-dimensional array.

A 2-D array is actually a 1-D array in which each element is itself a 1-D array. So arr is an array of 3 elements where each element is a 1-D array of 4 integers.

In the previous chapter, we have already discussed that the name of a 1-D array is a constant pointer to the 0th element. In the case, of a 2-D array, 0th element is a 1-D array. Hence in the above example, the type or base type of arr is a pointer to an array of 4 integers. Since pointer arithmetic is performed relative to the base size of the pointer. In the case of arr, if arr points to address 2000 then arr + 1 points to address 2016 (i.e 2000 + 4*4).

We know that the name of the array is a constant pointer that points to the 0th element of the array. In the case of a 2-D array, 0th element is a 1-D array. So the name of the array in case of a 2-D array represents a pointer to the 0th 1-D array. Therefore in this case arr is a pointer to an array of 4 elements. If the address of the 0th 1-D is 2000, then according to pointer arithmetic (arr + 1) will represent the address 2016, similarly (arr + 2) will represent the address 2032.

From the above discussion, we can conclude that:

arr points to 0th 1-D array.
(arr + 1) points to 1st 1-D array.
(arr + 2) points to 2nd 1-D array.

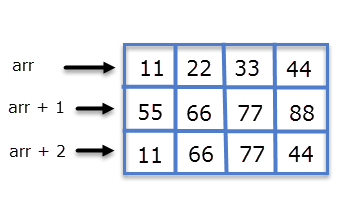
In general, we can write:

(arr + i) points to ith 1-D array.

As we discussed earlier in this chapter that dereferencing a pointer to an array gives the base address of the array. So dereferencing arr we will get *arr, base type of *arr is (int*). Similarly, on dereferencing arr+1 we will get *(arr+1). In general, we can say that:

*(arr+i) points to the base address of the ith 1-D array.

Again it is important to note that type (arr + i) and *(arr+i) points to same address but their base types are completely different. The base type of (arr + i) is a pointer to an array of 4 integers, while the base type of *(arr + i) is a pointer to int or (int*).

So how you can use arr to access individual elements of a 2-D array?

Since *(arr + i) points to the base address of every ith 1-D array and it is of base type pointer to int, by using pointer arithmetic we should we able to access elements of ith 1-D array.

Let's see how we can do this:

*(arr + i) points to the address of the 0th element of the 1-D array. So,
*(arr + i) + 1 points to the address of the 1st element of the 1-D array
*(arr + i) + 2 points to the address of the 2nd element of the 1-D array

Hence we can conclude that:

*(arr + i) + j points to the base address of jth element of ith 1-D array.

On dereferencing *(arr + i) + j we will get the value of jth element of ith 1-D array.

*( *(arr + i) + j)

By using this expression we can find the value of jth element of ith 1-D array.

Furthermore, the pointer notation *(*(arr + i) + j) is equivalent to the subscript notation.

The following program demonstrates how to access values and address of elements of a 2-D array using pointer notation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include<stdio.h>

int main()
{
    int arr[3][4] = {
                        {11,22,33,44},
                        {55,66,77,88},
                        {11,66,77,44}
                    };

    int i, j;

    for(i = 0; i < 3; i++)
    {
        printf("Address of %d th array %u \n",i , *(arr + i));
        for(j = 0; j < 4; j++)
        {
             printf("arr[%d][%d]=%d\n", i, j, *( *(arr + i) + j) );
        }
        printf("\n\n");
    }

    // signal to operating system program ran fine
    return 0;
}

Expected Output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

Address of 0 th array 2686736
arr[0][0]=11
arr[0][1]=22
arr[0][2]=33
arr[0][3]=44

Address of 1 th array 2686752
arr[1][0]=55
arr[1][1]=66
arr[1][2]=77
arr[1][3]=88

Address of 2 th array 2686768
arr[2][0]=11
arr[2][1]=66
arr[2][2]=77
arr[2][3]=44

Assigning 2-D Array to a Pointer Variable #

You can assign the name of the array to a pointer variable, but unlike 1-D array you will need pointer to an array instead of pointer to int or (int *) . Here is an example:

1
2
3
4

int arr[2][3] = {
                    {33, 44, 55},
                    {11, 99, 66}
                };

Always remember a 2-D array is actually a 1-D array where each element is a 1-D array. So arr as an array of 2 elements where each element is a 1-D arr of 3 integers. Hence to store the base address of arr, you will need a pointer to an array of 3 integers.

Similarly, If a 2-D array has 3 rows and 4 cols i.e int arr[3][4], then you will need a pointer to an array of 4 integers.

int (*p)[3];

Here p is a pointer to an array of 3 integers. So according to pointer arithmetic p+i points to the ith 1-D array, in other words, p+0 points to the 0th 1-D array, p+1 points to the 1st 1-D array and so on. The base type of (p+i) is a pointer to an array of 3 integers. If we dereference (p+i) then we will get the base address of ith 1-D array but now the base type of *(p + i) is a pointer to int or (int *). Again to access the address of jth element ith 1-D array, we just have to add j to *(p + i). So *(p + i) + j points to the address of jth element of ith 1-D array. Therefore the expression *(*(p + i) + j) gives the value of jth element of ith 1-D array.

The following program demonstrates how to access elements of a 2-D array using a pointer to an array.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include<stdio.h>

int main()
{
    int arr[3][4] = {
                        {11,22,33,44},
                        {55,66,77,88},
                        {11,66,77,44}
                    };

    int i, j;
    int (*p)[4];

    p = arr;

    for(i = 0; i < 3; i++)
    {
        printf("Address of %d th array %u \n",i , p + i);
        for(j = 0; j < 4; j++)
        {
            printf("arr[%d][%d]=%d\n", i, j, *( *(p + i) + j) );
        }
        printf("\n\n");
    }

    // signal to operating system program ran fine
    return 0;
}

Expected Output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

Address of 0 th array 2686736
arr[0][0]=11
arr[0][1]=22
arr[0][2]=33
arr[0][3]=44

Address of 1 th array 2686752
arr[1][0]=55
arr[1][1]=66
arr[1][2]=77
arr[1][3]=88

Address of 2 th array 2686768
arr[2][0]=11
arr[2][1]=66
arr[2][2]=77
arr[2][3]=44